1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
| import torch
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1)
y = x.pow(2) + 0.2*torch.rand(x.size())
def save():
net1 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)
loss_func = torch.nn.MSELoss()
for t in range(100):
prediction = net1(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
plt.figure(1, figsize=(10, 3))
plt.subplot(131)
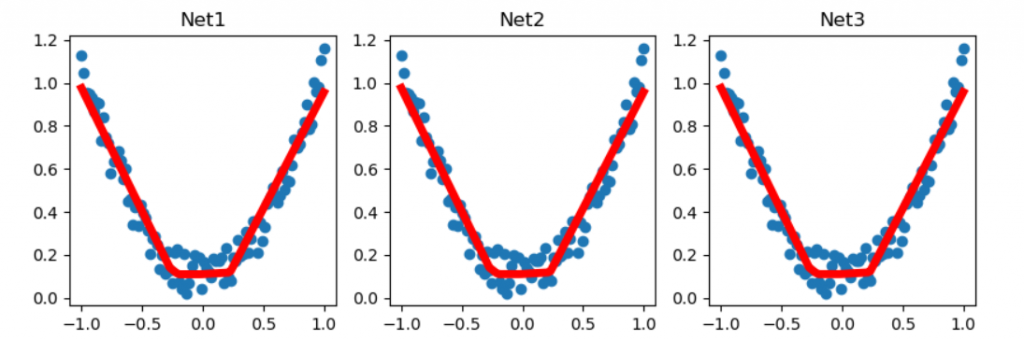
plt.title('Net1')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
torch.save(net1, 'net.pkl')
torch.save(net1.state_dict(), 'net_params.pkl')
def restore_net():
net2 = torch.load('net.pkl')
prediction = net2(x)
plt.subplot(132)
plt.title('Net2')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
def restore_params():
net3 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)
plt.subplot(133)
plt.title('Net3')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.show()
save()
restore_net()
restore_params()
|