堆的基本操作：插入元素、删除最大元素

最大堆结构定义

class Heap
{
    vector<int> vec;//用向量来构造堆
    public:
    Heap() {}
    ~Heap(){}
    void insert(int n);//插入
    void erase();//删除最大值
    void display();//按层次输出，方便验证程序是否正确
};

插入（添加在尾部，上调）

void Heap::insert(int n)
{
    vec.push_back(n);           //向量末尾加一个元素
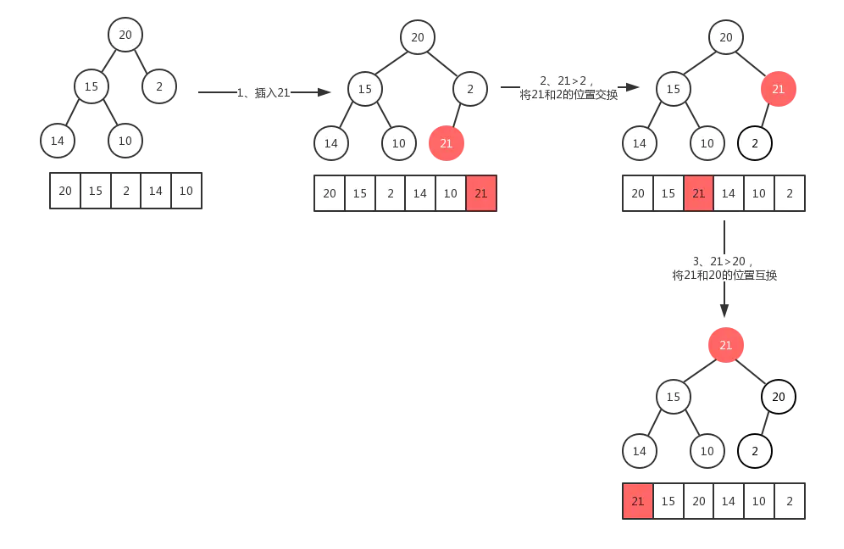
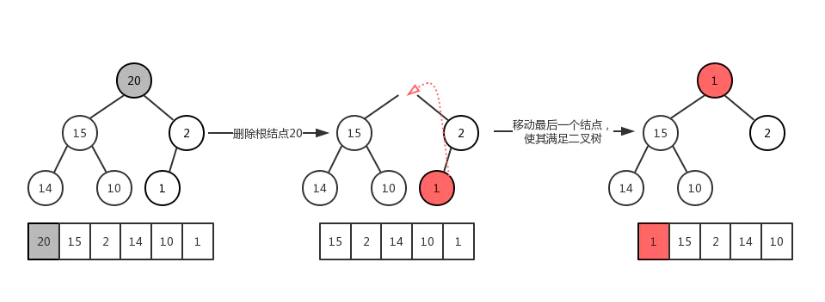
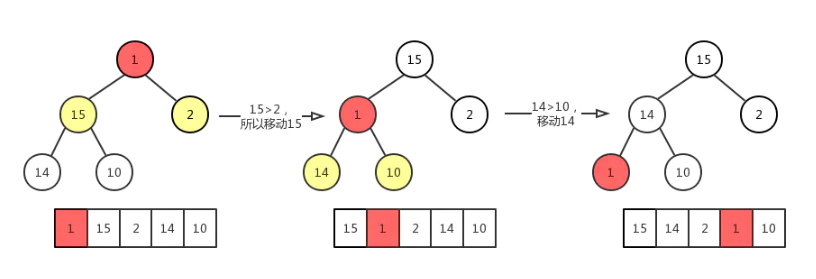
    int s = int(vec.size()) - 1; //获取元素个数
    while (vec[(s - 1) / 2] < vec[s])
    {
        swap(vec[(s - 1) / 2], vec[s]); //和父节点元素交换
        s = (s - 1) / 2;                    //定位到原父节点位置
        if (s == 0)
            break;
    }
}

删除最大元素（删除根，末尾节点浮上，再下调）

每次下调，与左右节点中大的那个交换

void Heap::erase()
{
    if (vec.empty()) //向量为空，直接返回
        return;
    int s = int(vec.size());
    swap(vec[0], vec[s - 1]); //交换首尾元素
    vec.pop_back();              //删除末尾元素
    s -= 1;
    int i = 0;
    while (1) //对根节点执行下调
    {
        if ((2 * i + 1) <= (s - 1)) //左节点存在
        {
            if ((2 * i + 2) <= s - 1) //右节点存在
            {
                if (vec[i] < vec[2 * i + 1] && vec[i] < vec[2 * i + 2]) //比两个子节点都小
                {
                    int temp = vec[2 * i + 1] < vec[2 * i + 2] ? (2 * i + 2) : (2 * i + 1);
                    swap(vec[i], vec[temp]); //和大的那个子节点交换
                    i = temp;
                }
                else if (vec[i] < vec[2 * i + 1]) //比左节点小，比右节点大
                {
                    swap(vec[i], vec[2 * i + 1]); //和左子节点交换
                    i = 2 * i + 1;
                }
                else if (vec[i] < vec[2 * i + 2]) //比右节点小，比左节点大
                {
                    swap(vec[i], vec[2 * i + 2]); //和右子节点交换
                    i = 2 * i + 2;
                }
                else //比左右节点都大
                    break;
            }
            else //不存在右节点
            {
                if (vec[i] < vec[2 * i + 1])
                {
                    swap(vec[i], vec[2 * i + 1]); //和左子节点交换
                    i = 2 * i + 1;
                }
                else //比左节点大
                    break;
            }
        }
        else //没有左节点
            break;
    }
}