哈夫曼树，编码解码

定义

给定N个权值作为N个叶子结点，构造一棵二叉树，若该树的带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

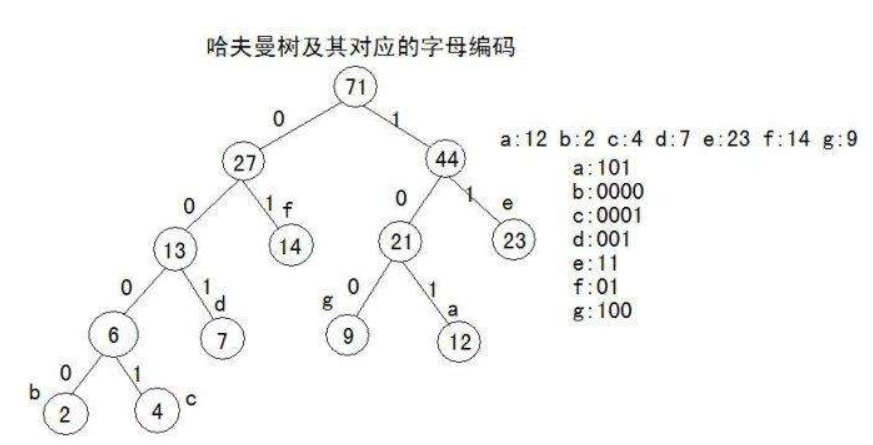
树结构

class Node
{
public:
    char c;     //字符
    int weight; //权重
    Node *left;
    Node *right;
    Node *parent;
    Node(char cc, int w) //叶子节点构造函数
    {
        c = cc;
        weight = w;
        left = NULL;
        right = NULL;
        parent = NULL;
    }
    Node(int w, Node *l, Node *r, Node *p) //非叶子节点构造函数
    {
        c = ' ';
        weight = w;
        left = l;
        right = r;
        parent = p;
    }
};
class HuffmanTree
{
    Node *root;

public:
    HuffmanTree() { root = NULL; }
    ~HuffmanTree() { release(root); }
    void release(Node *root);        //用于析构释放内存
    void setTree(vector<Node *> &v); //生成哈夫曼树
    void enCode(string s);           //编码
    void deCode(string str);         //解码
};

构造树

void HuffmanTree::setTree(vector<Node *> &v)
{ //传入参数为节点向量，结合测试用例看
    sort(v.begin(), v.end(), cmp);
    while (int(v.size() != 1))
    {
        int n = int(v.size()) - 1;
        Node *p1 = v[n];
        Node *p2 = v[n - 1];
        //排序后，以最后两个元素，new一个新节点，新节点权重等于两个子节点权重之和
        Node *temp = new Node((p1->weight + p2->weight), p1, p2, NULL);
        p1->parent = temp; //最后两个元素的父节点为新节点
        p2->parent = temp;
        v.erase(v.end() - 1); //移除最后两个元素，（没有释放对象内存）
        v.erase(v.end() - 1);
        v.push_back(temp);             //把新节点放进向量中
        sort(v.begin(), v.end(), cmp); //重新排序
    }
    root = v[0]; //向量中只剩下一个元素时，该节点就是哈夫曼树根
}
bool cmp(Node *p1, Node *p2) //向量排序时的自定义规则
{
    return p1->weight > p2->weight;
}

编码

void HuffmanTree::enCode(string str)
{
    Node *p = root;
    if (!p)
        return;
    stack<Node *> s;
    vector<Node> v;
    //以下为非递归前序遍历
    s.push(root);
    while (!s.empty())
    {
        Node *temp = s.top();
        if (!temp->left && !temp->right) //是叶子节点
            v.push_back(*temp);          //放进向量中
        s.pop();                         //弹出栈顶元素
        if (temp->right)                 //右节点不空
        {
            s.push(temp->right); //入栈
        }
        if (temp->left) //左节点不空
        {
            s.push(temp->left); //入栈
        }
    }
    //以上遍历后所有叶子节点存进了一个向量中
    for (int i = 0; i < int(str.length()); i++)
    {
        for (int j = 0; j < int(v.size()); j++) //在向量中查找
            if (v[j].c == str[i])               //目标叶子节点的字符和传递进来的字符相同
            {
                //执行编码算法
                stack<char> stk;
                Node *cur;
                cur = &v[j];
                while (cur) //从叶子节点向根回溯路径，每一步压入栈
                {
                    if (cur->parent)
                    {
                        if (cur->parent->left->weight == cur->weight) //是左节点，标记路径为0
                        {
                            stk.push('0');
                        }
                        else //是右节点，标记路径为1
                            stk.push('1');
                    }
                    cur = cur->parent; //回溯一步
                }
                while (!stk.empty()) //输出栈中所有元素，即为根到叶子节点的路径
                {
                    cout << stk.top();
                    stk.pop();
                }
                cout << ' '; //每个字符编码输出间空一格，方便查看验证
            }
    }
    cout << endl;
}

解码

void HuffmanTree::deCode(string str)
{
    Node *p = root;
    if (!p)
        return;
    for (int i = 0; i < int(str.length()); i++)
    {
        if (str[i] == '0')                       //读到0
            p = p->left;                         //指针指向左节点
        else if (str[i] == '1')                  //读到1
            p = p->right;                        //指针指向右节点
        if (p->left == NULL && p->right == NULL) //是叶子节点
        {
            cout << p->c; //输出字符
            p = root;     //指针重新指向根节点
        }
    }
    cout << 'n';
}

测试用例

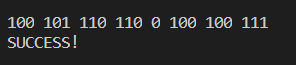
void test()
{
    vector<Node *> v;
    v.push_back(new Node('S', 5));
    v.push_back(new Node('U', 8));
    v.push_back(new Node('C', 9));
    v.push_back(new Node('E', 20));
    v.push_back(new Node('!', 10));
    HuffmanTree t;
    t.setTree(v);

    // cout << "输入为:SUCCESS!n编码为:";
    t.enCode("SUCCESS!");

    // cout << "输入为:1001011101100100100111n解码为:";
    t.deCode("1001011101100100100111"); //上一步中的编码反过来解析

    cout << "nn";
}

结果