本文最后更新于 2024年10月2日 上午
汉诺塔
如下图所示,从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数

n == 1
第1次 1号盘 A—->C sum = 1
n == 2
第1次 1号盘 A—->B
第2次 2号盘 A—->C
第3次 1号盘 B—->C sum = 3
n == 3
第1次 1号盘 A—->C
第2次 2号盘 A—->B
第3次 1号盘 C—->B
第4次 3号盘 A—->C
第5次 1号盘 B—->A
第6次 2号盘 B—->C
第7次 1号盘 A—->C sum = 7
到此可以发现需要移动的次数为2^n-1(n是圆盘个数)
还可以发现,如果我把n个盘子的问题记为X,n-1个盘子的问题记为Y,那么问题X可以视作两个问题Y再加上“移动一次最大的盘子”这一个步骤:
1.把上面n-1个盘子从A移动到B,(B和C完全等价,这一步可以视作是一个问题Y的解决过程)
2.把最大盘从A移动到C
3.把B上的n-1个盘子移动到C,同理这也是一个问题Y的解决过程
解释成代码如下
1
2
3
4
5
6
7
8
9
10
11
| void hanoi(int n, char A, char B, char C)
{
if (n == 1)
move(A, C);
else
{
hanoi(n - 1, A, C, B);
move(A, C);
hanoi(n - 1, B, A, C);
}
}
|
以上参考https://blog.csdn.net/qq_19446965/article/details/81591945
数制转换(十进制转任意进制)
1
2
3
4
5
6
7
8
9
| string conversion(int m, int n)
{
string table = "0123456789ABCDEF";
string c(1,table[m % n]);
if (m / n == 0)
return c + "";
else
return conversion(m / n, n) + c;
}
|
今天翻出了初学数据结构时写的非递归版本的任意进制的数制转换,还有字符栈的显示,感觉还可以,也贴在下面
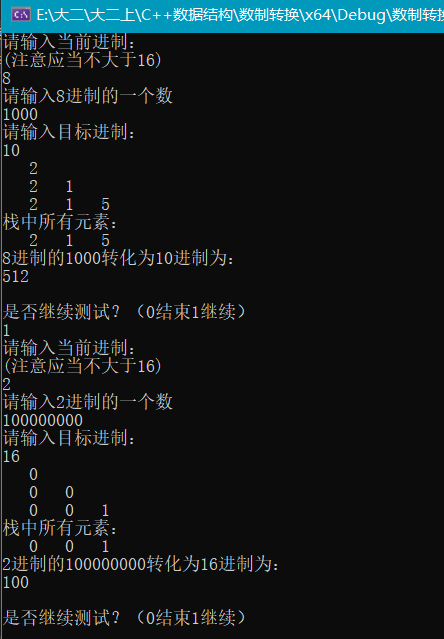
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
| #include <iostream>
#include <iomanip>
#include <string>
#include <cmath>
using namespace std;
template <typename T>
class stack
{
int size;
int capacity;
T *stk;
public:
stack();
~stack();
T Pop();
void Push(T);
bool Empty();
T Top();
int Size();
void Display();
};
template <typename T>
stack<T>::stack()
{
size = 0;
capacity = 1;
stk = new T[capacity];
}
template <typename T>
stack<T>::~stack()
{
delete[] stk;
}
template <typename T>
T stack<T>::Pop()
{
size--;
return stk[size];
}
template <typename T>
void stack<T>::Push(T i)
{
if (size == capacity)
{
capacity *= 2;
char *temp = new T[capacity];
for (int i = 0; i < size; i++)
{
temp[i] = stk[i];
}
T *p = stk;
stk = temp;
delete[] p;
}
stk[size++] = i;
}
template <typename T>
T stack<T>::Top()
{
return stk[size - 1];
}
template <typename T>
bool stack<T>::Empty()
{
return size == 0;
}
template <typename T>
int stack<T>::Size()
{
return size;
}
template <typename T>
void stack<T>::Display()
{
for (int i = 0; i < size; i++)
cout << setw(4) << stk[i];
cout << '\n';
}
template <typename T>
void Converter(stack<T> &S)
{
char ch[16] = {'0', '1', '2', '3', '4', '5', '6', '7', '8', '9', 'A', 'B', 'C', 'D', 'E', 'F'};
int c1, c2;
int x = 0;
string s1;
cout << "请输入当前进制:\n(注意应当不大于16)\n";
cin >> c1;
while (cin.fail() c1 > 16c1 < 1)
{
cout << "\n输入不正确,请重新输入:\n";
cin >> c1;
}
cout << "请输入" << c1 << "进制的一个数\n";
cin >> s1;
while (cin.fail())
{
cout << "\n输入不正确,请重新输入:\n";
cin >> s1;
}
for (int i = int(s1.length() - 1); i >= 0; i--)
{
if (s1[i] >= '0' && s1[i] <= '9')
{
x += int((s1[i] - '0')* pow(c1, s1.length() - i - 1));
}
else if (s1[i] >= 'A' && s1[i] <= 'F')
{
x += int((s1[i] - 'A' + 10)* pow(c1, s1.length() - i - 1));
}
}
cout << "请输入目标进制:\n";
cin >> c2;
while (cin.fail() c1 > 16 c1 < 1)
{
cout << "\n输入不正确,请重新输入:\n";
cin >> c2;
}
while (x)
{
S.Push(ch[x % c2]);
x /= c2;
S.Display();
}
cout << "栈中所有元素:\n";
S.Display();
cout << c1 << "进制的" << s1 << "转化为" << c2 << "进制为:\n";
while (!S.Empty())
{
cout << S.Top();
S.Pop();
}
}
int main()
{
stack<char> S;
while (1)
{
Converter(S);
cout << "\n\n是否继续测试?(0结束1继续)\n";
int n;
cin >> n;
if (!n)
break;
}
return 0;
}
```
|

