中缀表达式转后缀表达式

从左向右扫描中缀表达式;
访问到操作数,加人后缀表达式;
访问到左括号“(“,立即入栈;
访问到右括号“)”,栈中操作符依次出栈并加入后缀表达式,直到出现左括号“(”,“(”出栈;
访问到除括号之外的其他操作符,当其优先级比栈顶除“(”之外的操作符高时入栈,否则比当前操作符优先级高或者优先级相等的操作符依次出栈。

使用一种不需要括号的表达式的图形表示法,称为表达式树。树使用圆圈代表存储数据的节点,这些节点之间由称为边的线段连接。在一棵表达式树中,每个节点要么包含一个操作数,要么包含一个运算符。每个包含二元运算符的节点都连接到两个称为子女的节点,包含运算符的节点就称为这两个子女节点的双亲。左边的子女包含这个运算符的第一个操作数，它被画在它双亲的左下方;右边的子女包含这个运算符的第二个操作数,被画在它双亲的右下方。

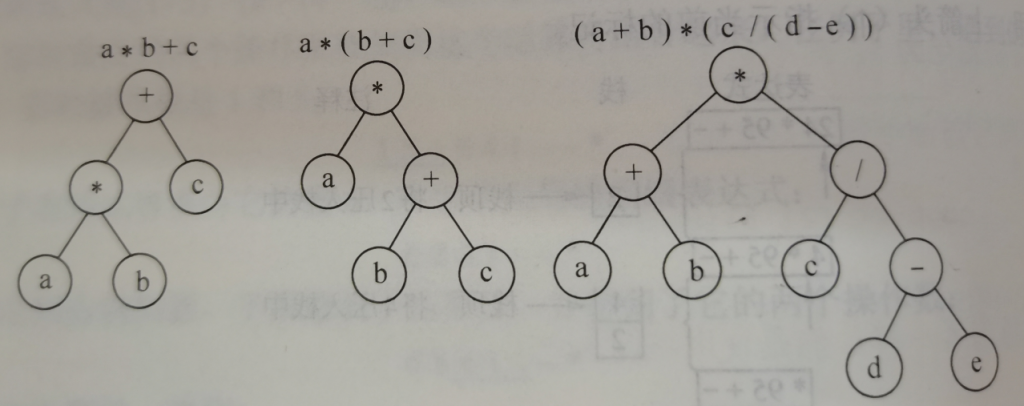
从这些例子可以看到中缀表达式是如何不使用括号而图形化表示的要得到和一棵表达式树相对应的后缀表达式,必须按照左-右-双亲节点的次序(后序)来遍历(也就是,走遍)这棵树。这意味着对于每一个节点,在可以“访问”它之前,必须首先访间它的左子女和右子女。对于中缀表达式a*b+c,这个遍历产生了如下图

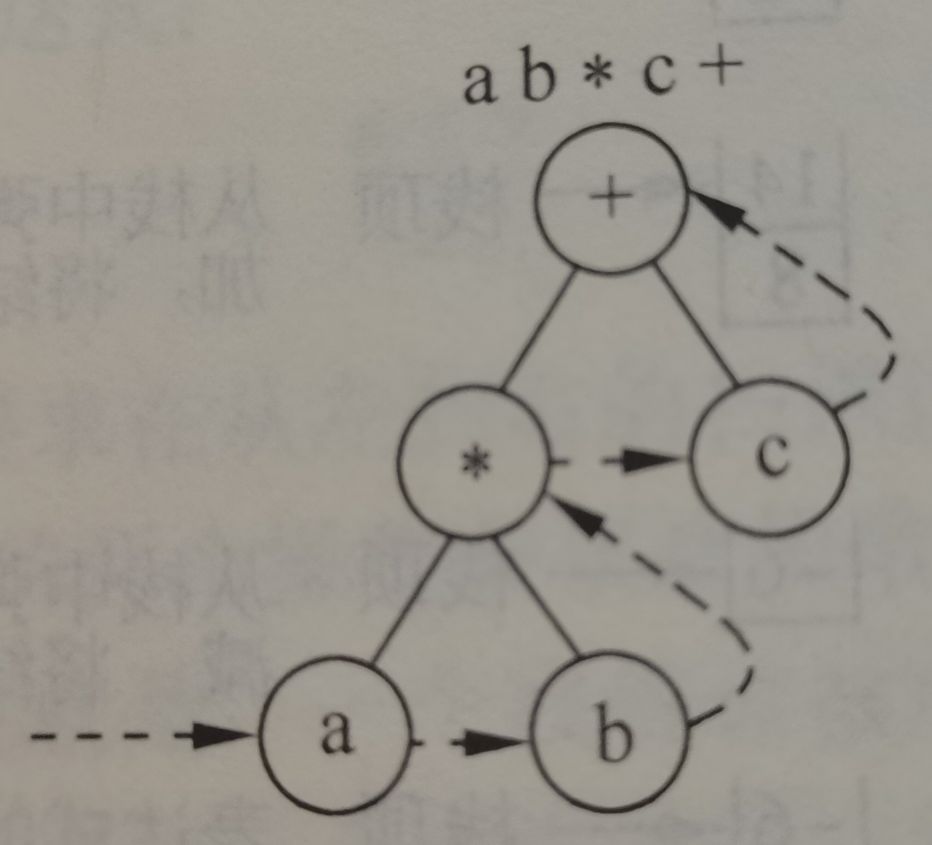
总结

1.画出表达式树

2.后序遍历