哈希（Hash）表（散列表）

哈希表定义

哈希表是一种根据关键码去寻找值的数据映射结构，最经典的例子就是字典，如果我想要获取“按”字详细信息，我肯定会去根据拼音an去查找拼音索引，在索引列表中找到an，发现它的页码是4。这就是一个键值映射过程，通过关键字key查找对应的值的索引f(key)。其中，关键字就是“按”，f(key)就是哈希函数，f(“按”)=4就是哈希值。

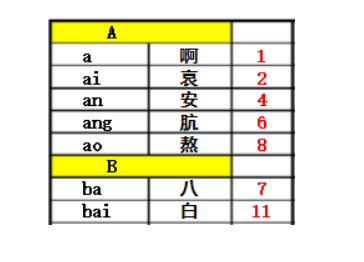
哈希表冲突（散列冲突）

但是问题又来了，我们要查的是“按”，而不是“安，但是他们的拼音都是一样的。也就是通过关键字按和关键字安可以映射到一样的字典页码4的位置，这就是哈希冲突（也叫哈希碰撞），在公式上表达就是key1≠key2，但f(key1)=f(key2)。冲突会给查找带来麻烦，你想想，你本来查找的是“按”，但是却找到“安”字，你又得向后翻一两页，在计算机里面也是一样道理的。

　　但哈希冲突是无可避免的，为什么这么说呢，因为你如果要完全避开这种情况，你只能每个字典去新开一个页，然后每个字在索引里面都有对应的页码，这就可以避免冲突。但是会导致空间增大（每个字都有一页）。

　　既然无法避免，就只能尽量减少冲突带来的损失，而一个好的哈希函数需要有以下特点：

　　1.尽量使关键字对应的记录均匀分配在哈希表里面（比如说某厂商卖30栋房子，均匀划分ABC，3个区域，如果你划分A区域1个房子，B区域1个房子，C区域28个房子，有人来查找C区域的某个房子最坏的情况就是要找28次）。

　　2.关键字极小的变化可以引起哈希值极大的变化。

常见的哈希函数

• 直接定制法：
  即取元素的某个线性函数为散列地址：Hash(key) = A*key +B;
  例如：找出字符串中只出现一次的字符。时间复杂度为O(N),空间复杂度为：O(1);(就可以使用该方法，开辟一个256个元素的数组，进行统计每个元素出现的次数)
  优点：简单，均匀
  适合于查找比较小而且连续的情况。
• 除留取余法：（比较常用的方法）
  Hash(key) = key % p;(p <= m && p 质数)，m为散列表中允许的地址个数。
• 平方取中法：
  对数据进行平方，然后取数据的中间3位为哈希地址。
  适合于：不知道数据的分布情况，但是数字又不是很大的情况

冲突处理策略

1.闭散列（放地址法）

线性探测法查找下一个位置:
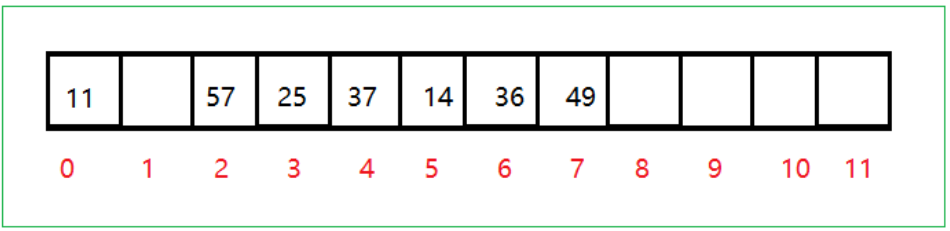
例如：关键码集合为：{37，25，14，36，49，57，11}，设表的长度为12，Hash(key) = key%p(p = 11);
Hash(37) = 4;
Hash(25) = 3;
Hash(14) = 3;
Hash(36) = 3;
Hash(49) = 5;
Hash(57) = 2;
Hash(11) = 0;
很明显：这组数据的哈希地址有冲突。
在插入时，如果该位置已经有元素了，就从该位置起向后找，找到一个空闲的位置就进行插入。
如下图所示：

二次探测法：
就是当有哈希冲突时，寻找下一个空闲位置时，首先在该位置处加1的平方，若加1的平方的位置处依然有元素，那就加2的平方，知道找到一个空闲的位置为止。

优点：简单 易懂
缺点：一旦发生了哈希冲突，所有的冲突连接在一起，很容易产生数据”堆积”。即不同的数据占用可以利用的位置，就使得寻找其余数据的位置需要进行多次比较，就会导致查找的效率降低。

2.开散列（链地址法）

上面所说的开发定址法的原理是遇到冲突的时候查找顺着原来哈希地址查找下一个空闲地址然后插入，但是也有一个问题就是如果空间不足，那他无法处理冲突也无法插入数据，因此需要装填因子(插入数据/空间)<=1。

　　那有没有一种方法可以解决这种问题呢？链地址法可以，先用哈希函数计算每个数据的散列地址，把具有相同地址的元素归于同一个集合之中，把该集合处理为一个链表，链表的头节点存储于哈希表之中。
例如：还是上面闭散列中的例子，当使用开散列的方法后，其每个元素的存储为下图所示：

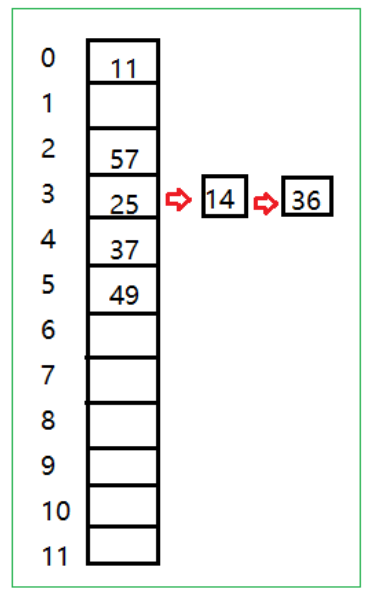
可见，开散列法有效的解决了数据溢出，不过需要增设链接指针，增加了存储的开销。但是，总体而言，效率还是快的多。

哈希表的性能

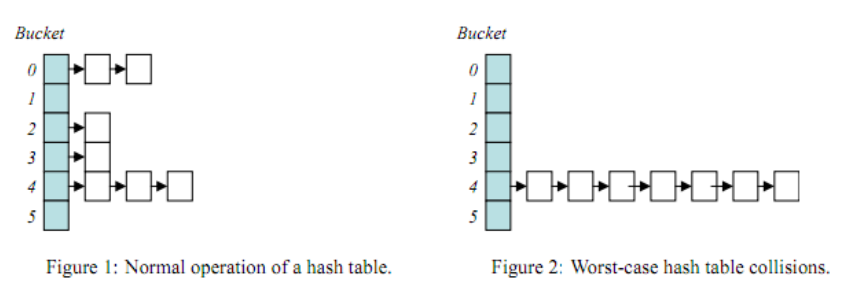
由于哈希表高效的特性，查找或者插入的情况在大多数情况下可以达到O(1)，时间主要花在计算hash上，当然也有最坏的情况就是hash值全都映射到同一个地址上，这样哈希表就会退化成链表，查找的时间复杂度变成O(n)，但是这种情况比较少，只要不要把hash计算的公式外漏出去并且有人故意攻击，一般也不会出现这种情况。

参考原文

https://www.cnblogs.com/s-b-b/p/6208565.html

https://blog.csdn.net/Yinghuhu333333/article/details/81364739